
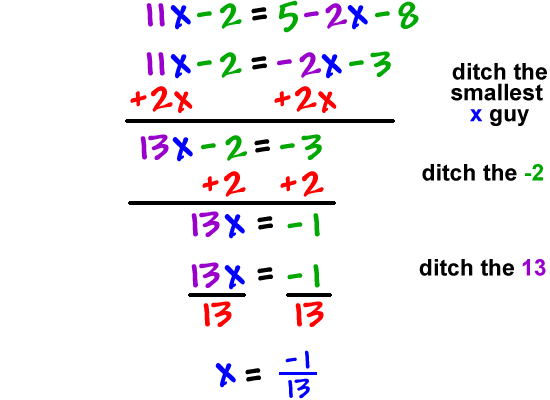
2 variable system of equations solver series#
This example uses the Substitution and Elimination techniques to solve simultaneous KVL loop equations and is illustrated step by step.In math and engineering, we often are left with a series of equations with an equal number of variables that we want to solve for. (Use Eq.1)Ī practical example of how these techniques are applied is provided in the video animation on Loop Analysis below. We would now use this known value of y in one of the original equations to solve for the value of x. If we write the equations one on top of the other, we can simply sum vertically to arrive at our single variable equation. Now we sum our two new equations to obtain an equation with a single variable. These will cancel each other out when the two equations are summed. If we multiply Eq.1 by 8 and Eq.2 by -3, the x terms become 24x and -24x respectively. In order to clear the x terms from the above equations, it will be necessary to apply a factor to both equations in order to create the situation we desire. We could have decided to eliminate the x variable instead, leaving an equation with y as the only unknown quantity. In this last example, we eliminated the y term from the equations because it was an easily recognizable means of reducing the equation to a single unknown. We would now use the value of 4 for x in either of the two original equations to solve for the value of y. To sum these equations, add the terms from the left hand side of each equation together, and add the terms from the right hand side of the equations together as follows…. Adding the -4y from the right side of our new expression for Eq.1 to the 4y on the right hand side of Eq.2 will result in 0y, which effectively eliminates the y term from the resulting equation.Įq.1 -6x – 4 = - 4y (modified Eq.1 by factor of -2) Now we will sum this new expression for Eq.1 with our original Eq.2. We selected -2 as the factor to multiply Eq.1 by so that the right hand side of Eq.1 when added to the right hand side of Eq.2 will result in the y term being eliminated from the resulting equation. If we multiply both sides of Eq.1 by a factor of -2 and then sum the two equations, we will be left with an expression containing only one unknown. This time, our objective is to find a factor to multiply one of the equations by which will allow us to sum the two equations and eliminate one of the unknowns. This approach can also be used to solve for the two unknowns in the same two equations. Y = 7 Using the Elimination Approach To Solve Simultaneous Equations Having the value of x, we can use it in Eq.1 or Eq.2 to find the value of y. This will leave us with only one unknown quantity, x, to solve for in Eq.2 instead of the two unknowns we had before. Since we now have an expression for the value of y in terms of x, we will replace/substitute the y term in Eq.2 with this new expression we obtained above. By this we mean, we need an equation that states the value of a single y in terms of x. We want to isolate the y term in one equation. Solve for x, and y given these two equations containing the two unknown quantities.

Using the Substitution Approach To Solve Simultaneous Equations We would require three equations to solve for three unknown quantities, and so on. For instance, we would require two equations to solve for two unknown quantities. In order to solve for a given number of unknowns, we require that the same number of equations be provided. The two technician level methods for solving simultaneous equations having multiple unknowns used when dealing with two or three equations are “substitution” and “elimination”. In this third installment of The Practicing Technicians Series, we will review a means of solving such equations to get loop currents or node voltages when performing linear DC network analysis. Many technicians encounter difficulty in solving node or loop equations containing multiple unknown quantities.
2 variable system of equations solver how to#
How to Solve Simultaneous Equations with Multiple Unknowns Topics of discussion will include circuit reduction techniques, transient responses, as well as areas of difficulty when working with linear dc network theorems. In this series, we will be discussing some everyday skills and topics for practicing technicians, as well as some areas that have been identified as “difficult to understand” by our technician students while performing general circuit analysis. This is the third in our series of brief articles discussing important topics relevant to electronics and electromechanical technicians and technician students preparing for today’s workforce.


 0 kommentar(er)
0 kommentar(er)
